Pipelines¶
Most of the time, we not only care about the performance of all the deployed indicators, but about the health of the entire backtesting pipeline in general - having an ultrafast indicator brings nothing if the main bottleneck is the portfolio simulator itself.
Let's build a simple pipeline that takes the input data and strategy parameters, and returns the Sharpe ratio per symbol and parameter combination:
>>> def pipeline(data, period=7, multiplier=3):
... high = data.get('High')
... low = data.get('Low')
... close = data.get('Close')
... st = SuperTrend.run(
... high,
... low,
... close,
... period=period,
... multiplier=multiplier
... )
... entries = (~st.superl.isnull()).vbt.signals.fshift()
... exits = (~st.supers.isnull()).vbt.signals.fshift()
... pf = vbt.Portfolio.from_signals(
... close,
... entries=entries,
... exits=exits,
... fees=0.001,
... save_returns=True, # (1)!
... max_order_records=0, # (2)!
... freq='1h'
... )
... return pf.sharpe_ratio # (3)!
>>> pipeline(data)
st_period st_multiplier symbol
7 3 BTCUSDT 1.521221
ETHUSDT 2.258501
Name: sharpe_ratio, dtype: float64
>>> %%timeit
>>> pipeline(data)
32.5 ms ± 1.12 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)
- Pre-calculate the returns
- Do not generate order records since we only need the returns
- Portfolio can automatically recognize that the returns were pre-computed and use them instead of computing them from scratch
The indicator takes roughly 3 milliseconds for both columns, or 10% of the total execution time. The other 90% are spent to select the data, create entries and exits, perform the simulation, and calculate the Sharpe values.
As you might have guessed, the simulation is the place where the most of the processing takes place: vectorbt has to update the cash balance, group value, and other metrics at every single time step to keep the trading environment intact. Finally, after finishing the simulation, it has to go over the data one to multiple times to reconstruct the attributes required for computing various statistics, usually including the cash flow, cash, asset flow, assets, asset value, portfolio value, and finally, returns. If we were to populate and keep all of this information during the simulation, we would run out of memory. But luckily for us, we can avoid the reconstruction phase entirely by pre-computing the returns, as we did above.
Now, guess what will be the execution time when running the same pipeline 336 times? You say 10 seconds?
>>> op_tree = (product, periods, multipliers)
>>> period_product, multiplier_product = vbt.generate_param_combs(op_tree) # (1)!
>>> period_product = np.asarray(period_product)
>>> multiplier_product = np.asarray(multiplier_product)
>>> %%timeit
>>> pipeline(data, period_product, multiplier_product)
2.38 s ± 142 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)
- Using generate_param_combs
Only 1/5 of that. This is because vectorbt knows how to process wide arrays efficiently. But as soon as you start testing thousands of parameter combinations, the performance will begin to suffer. Generally, stacking a lot of columns at once consumes much more memory than doing it in a loop, and as soon as you have used all the available memory, depending upon the system, the process switches to the swap memory, which is much slower to access than RAM. How do we tackle this?
Chunked pipeline¶
To avoid memory problems, let's make our pipeline chunkable. Chunking in vectorbt allows for splitting arguments (in our case, parameter combinations) such that only one bunch of the argument values is passed to the pipeline function at a time. This is done using the chunked decorator:
>>> chunked_pipeline = vbt.chunked(
... size=vbt.LenSizer(arg_query='period', single_type=int), # (1)!
... arg_take_spec=dict( # (2)!
... data=None, # (3)!
... period=vbt.ChunkSlicer(), # (4)!
... multiplier=vbt.ChunkSlicer()
... ),
... merge_func=lambda x: pd.concat(x).sort_index() # (5)!
... )(pipeline)
- Get the total number of values to be chunked, by measuring the length of
periodusing LenSizer. Ifperiodis an integer, consider it as a single value. - Specification for splitting any argument passed to the
pipelinefunction - Pass the data as-is (i.e., without splitting)
- Slice the values of each parameter into chunks using ChunkSlicer
- Each chunk returns a Series with Sharpe values - concatenate the list of Series returned by all chunks using Pandas and sort the resulting Series
The returned chunked_pipeline function has the signature (i.e., accepted arguments and the order they come in) identical to that of the pipeline, but now it can internally split all arguments thanks to the chunking specification that we provided. It measures the number of elements in period and, by default, generates the same number of chunks as we have cores in our system. Each chunk contains the same input data passed as data (only a reference, not a copy!), and a slice of the values in period and multiplier. After all chunks have been processed, it merges their results using Pandas, such that we get the same result as if we had processed all parameter combinations at once. Incredible, right?
Let's test the chunked pipeline on one combination:
st_period st_multiplier symbol
7 3 BTCUSDT 1.521221
ETHUSDT 2.258501
Name: sharpe_ratio, dtype: float64
We're getting the same results as by using pipeline, which isn't much surprising. How about multiple combinations? Let's execute chunked_pipeline on 4 combinations split into 2 chunks while also showing the progress bar:
>>> chunked_pipeline(
... data,
... period_product[:4],
... multiplier_product[:4],
... _n_chunks=2, # (1)!
... )
- Any argument passed to the chunked decorator can be overridden during the runtime using the same argument but prefixed with an underscore
_
st_period st_multiplier symbol
4 2.0 BTCUSDT 0.451699
ETHUSDT 1.391032
2.1 BTCUSDT 0.495387
ETHUSDT 1.134741
2.2 BTCUSDT 0.985946
ETHUSDT 0.955616
2.3 BTCUSDT 1.193179
ETHUSDT 1.307505
Name: sharpe_ratio, dtype: float64
How do we know whether the passed arguments were split correctly?
>>> chunk_meta, tasks = chunked_pipeline(
... data,
... period_product[:4],
... multiplier_product[:4],
... _n_chunks=2,
... _return_raw_chunks=True
... )
>>> chunk_meta # (1)!
[ChunkMeta(uuid='0882b000-52ab-4694-bb7c-341a9370937b', idx=0, start=0, end=2, indices=None),
ChunkMeta(uuid='1d5a74d9-d517-437d-a20a-4580f601a280', idx=1, start=2, end=4, indices=None)]
>>> list(tasks) # (2)!
[(<function __main__.pipeline(data, period=7, multiplier=3)>,
(<vectorbtpro.data.custom.hdf.HDFData at 0x7f7b30509a60>,
array([4, 4]),
array([2., 2.1])),
{}),
(<function __main__.pipeline(data, period=7, multiplier=3)>,
(<vectorbtpro.data.custom.hdf.HDFData at 0x7f7b30509a60>,
array([4, 4]),
array([2.2, 2.3])),
{})]
- Generated chunks of type ChunkMeta. Arguments
periodandmultiplierwere sliced based onstartandend. - Each chunk has the same data but different set of parameter combinations
The first chunk contains the combinations (4, 2.0) and (4, 2.1), the second chunk contains the combinations (4, 2.2) and (4, 2.3).
And here's how long does it take to run all combinations of parameters:
>>> %%timeit
>>> chunked_pipeline(data, period_product, multiplier_product)
2.33 s ± 50.9 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)
We don't observe any increase in performance because there is no multiprocessing or multithreading taking place, but splitting into chunks is all about memory and keeping its health at maximum. But don't overdo! Looping over all parameter combinations and processing only one combination at a time is much slower because now vectorbt can't take advantage of multidimensionality:
>>> %%timeit
>>> chunked_pipeline(data, period_product, multiplier_product, _chunk_len=1)
11.4 s ± 965 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)
What's better? Something in-between. Usually, the default values are good enough.
Numba pipeline¶
Wouldn't it be great if we could parallelize our pipeline the same way as we did with the indicator? Unfortunately, our Python code wouldn't make the concurrency possible since it holds the GIL. But remember how Numba can release the GIL to enable multithreading? If only we could write the entire pipeline in Numba... Let's do this!
>>> @njit(nogil=True)
... def pipeline_nb(high, low, close,
... periods=np.asarray([7]), # (1)!
... multipliers=np.asarray([3]),
... ann_factor=365):
...
... # (2)!
... sharpe = np.empty(periods.size * close.shape[1], dtype=np.float_)
... long_entries = np.empty(close.shape, dtype=np.bool_)
... long_exits = np.empty(close.shape, dtype=np.bool_)
... group_lens = np.full(close.shape[1], 1)
... init_cash = 100.
... fees = 0.001
... k = 0
...
... for i in range(periods.size):
... for col in range(close.shape[1]):
... _, _, superl, supers = superfast_supertrend_nb( # (3)!
... high[:, col],
... low[:, col],
... close[:, col],
... periods[i],
... multipliers[i]
... )
... long_entries[:, col] = vbt.nb.fshift_1d_nb( # (4)!
... ~np.isnan(superl),
... fill_value=False
... )
... long_exits[:, col] = vbt.nb.fshift_1d_nb(
... ~np.isnan(supers),
... fill_value=False
... )
...
... sim_out = vbt.pf_nb.from_signals_nb( # (5)!
... target_shape=close.shape,
... group_lens=group_lens,
... init_cash=init_cash,
... high=high,
... low=low,
... close=close,
... long_entries=long_entries,
... long_exits=long_exits,
... fees=fees,
... save_returns=True
... )
... returns = sim_out.in_outputs.returns
... _sharpe = vbt.ret_nb.sharpe_ratio_nb(returns, ann_factor, ddof=1) # (6)!
... sharpe[k:k + close.shape[1]] = _sharpe # (7)!
... k += close.shape[1]
...
... return sharpe
- When using Numba, we cannot make an argument that can be both a scalar or an array - we need to decide for one data type. So, let's switch to using arrays only.
- Many arrays have a fixed shape, thus create them outside the loop
- Run
superfast_supertrend_nbon each column - Shift the signals one tick forward
- Using from_signals_nb
- Using sharpe_ratio_nb
- Output array
sharpestores an element per column and parameter combination
Running this pipeline on one parameter combination yields two (already familiar to us) Sharpe values, one per column in high, low, and close:
>>> ann_factor = vbt.pd_acc.returns.get_ann_factor(freq='1h') # (1)!
>>> pipeline_nb(
... high.values,
... low.values,
... close.values,
... ann_factor=ann_factor
... )
array([1.521221, 2.25850084])
>>> %%timeit
>>> pipeline_nb(
... high.values,
... low.values,
... close.values,
... ann_factor=ann_factor
... )
3.13 ms ± 544 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
- Get the annualization factor using ReturnsAccessor.get_ann_factor
One iteration of pipeline_nb is already 10x faster than one iteration of pipeline.
The next step is creation of a chunked pipeline. Since the returned values aren't Pandas Series anymore, we can't simply join them and hope for the best: we need to manually concatenate them and build a multi-level index for later analysis.
>>> def merge_func(arrs, ann_args, input_columns): # (1)!
... arr = np.concatenate(arrs)
... param_index = vbt.stack_indexes(( # (2)!
... pd.Index(ann_args['periods']['value'], name='st_period'),
... pd.Index(ann_args['multipliers']['value'], name='st_multiplier')
... ))
... index = vbt.combine_indexes(( # (3)!
... param_index,
... input_columns
... ))
... return pd.Series(arr, index=index) # (4)!
>>> nb_chunked = vbt.chunked(
... size=vbt.ArraySizer(arg_query='periods', axis=0), # (5)!
... arg_take_spec=dict(
... high=None, # (6)!
... low=None,
... close=None,
... periods=vbt.ArraySlicer(axis=0),
... multipliers=vbt.ArraySlicer(axis=0),
... ann_factor=None
... ),
... merge_func=merge_func,
... merge_kwargs=dict(
... ann_args=vbt.Rep("ann_args")
... )
... )
>>> chunked_pipeline_nb = nb_chunked(pipeline_nb)
- The merging function takes a list of one-dimensional NumPy arrays returned by the pipeline - one per chunk. Using
merge_kwargs, we also requested the annotated arguments to access the passed parameter values. Also, to combine parameter labels with column labels, we need the column labels to be specified (manually at each run). - Stack the parameter labels (since all parameter values at the same position build one parameter combination)
- Build the product of the parameter labels and the symbol labels (since one parameter combination is applied each symbol)
- Return the final array as a Series
- We don't provide
single_typeargument anymore to accept only arrays - We need to pass three two-dimensional NumPy arrays instead of
data, which has a complex Python type not recognized by Numba
Let's test the pipeline on four parameter combinations as we did with the previous pipeline:
>>> chunked_pipeline_nb(
... high.values,
... low.values,
... close.values,
... periods=period_product[:4],
... multipliers=multiplier_product[:4],
... ann_factor=ann_factor,
... _n_chunks=2,
... _merge_kwargs=dict(input_columns=close.columns)
... )
st_period st_multiplier symbol
4 2.0 BTCUSDT 0.451699
ETHUSDT 1.391032
2.1 BTCUSDT 0.495387
ETHUSDT 1.134741
2.2 BTCUSDT 0.985946
ETHUSDT 0.955616
2.3 BTCUSDT 1.193179
ETHUSDT 1.307505
dtype: float64
We can instantly recognize the values produced by the previous pipeline. Moreover, if you run the code, you'll also notice that chunked_pipeline_nb has the average iteration speed of 50 per second as compared to 15 per second of chunked_pipeline - a remarkable jump in performance. But that's not all: let's benchmark this pipeline without and with parallelization enabled.
>>> %%timeit
>>> chunked_pipeline_nb(
... high.values,
... low.values,
... close.values,
... periods=period_product,
... multipliers=multiplier_product,
... ann_factor=ann_factor,
... _merge_kwargs=dict(input_columns=close.columns)
... )
894 ms ± 14.6 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)
>>> %%timeit
>>> chunked_pipeline_nb(
... high.values,
... low.values,
... close.values,
... periods=period_product,
... multipliers=multiplier_product,
... ann_factor=ann_factor,
... _execute_kwargs=dict(engine="dask"),
... _merge_kwargs=dict(input_columns=close.columns)
... )
217 ms ± 4.67 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)
We just processed 12 million data points in 217 milliseconds, and that's in Python!
Contextualized pipeline¶
But it's not always about performance. Consider a scenario where we need to know the Sharpe ratio at each single time step to drive our trading decisions. This isn't possible using the pipelines we wrote above because we have introduced a path dependency: the current Sharpe now directly depends upon the previous Sharpe.
Exactly for such situations vectorbt designed a concept of a custom order function - a regular callback that can be executed at any time during the simulation. It takes a surrounding simulation context such as the running cash balance and makes a decision on whether to issue an order or not. Order functions are not the only callback inhabitants in vectorbt: there is an entire zoo of callbacks that can be called at specific checkpoints during the runtime. Using such callbacks is usually associated with a noticeable performance hit (still very fast though), but they make the event-driven backtesting possible in a package otherwise focused on manipulating arrays.
To make the simulation as fast as possible, we'll calculate both the SuperTrend and the Sharpe ratio in a single pass. This way, not only we will know those two values at each time step, but we will also retain the full control over their calculation.
Streaming Sharpe¶
We've already designed a streaming SuperTrend indicator, but what about Sharpe? Making it a one-pass algorithm requires implementing an accumulator, which is a fairly easy task because the Sharpe ratio essentially depends on the rolling mean and the standard deviation. Thus, we'll make an accumulator by simply combining other two accumulators: rolling_mean_acc_nb and rolling_std_acc_nb. If you followed me through the implementation of the streaming SuperTrend, you would have no difficulties understanding the following code:
>>> class RollSharpeAIS(tp.NamedTuple):
... i: int
... ret: float
... pre_window_ret: float
... cumsum: float
... cumsum_sq: float
... nancnt: int
... window: int
... minp: tp.Optional[int]
... ddof: int
... ann_factor: float
>>> class RollSharpeAOS(tp.NamedTuple):
... cumsum: float
... cumsum_sq: float
... nancnt: int
... value: float
>>> @njit(nogil=True)
... def rolling_sharpe_acc_nb(in_state):
... # (1)!
... mean_in_state = vbt.nb.RollMeanAIS(
... i=in_state.i,
... value=in_state.ret,
... pre_window_value=in_state.pre_window_ret,
... cumsum=in_state.cumsum,
... nancnt=in_state.nancnt,
... window=in_state.window,
... minp=in_state.minp
... )
... mean_out_state = vbt.nb.rolling_mean_acc_nb(mean_in_state)
...
... # (2)!
... std_in_state = vbt.nb.RollStdAIS(
... i=in_state.i,
... value=in_state.ret,
... pre_window_value=in_state.pre_window_ret,
... cumsum=in_state.cumsum,
... cumsum_sq=in_state.cumsum_sq,
... nancnt=in_state.nancnt,
... window=in_state.window,
... minp=in_state.minp,
... ddof=in_state.ddof
... )
... std_out_state = vbt.nb.rolling_std_acc_nb(std_in_state)
...
... # (3)!
... mean = mean_out_state.value
... std = std_out_state.value
... if std == 0:
... sharpe = np.nan
... else:
... sharpe = mean / std * np.sqrt(in_state.ann_factor)
...
... # (4)!
... return RollSharpeAOS(
... cumsum=std_out_state.cumsum,
... cumsum_sq=std_out_state.cumsum_sq,
... nancnt=std_out_state.nancnt,
... value=sharpe
... )
- Calculate the mean of the window
- Calculate the standard deviation of the window
- Calculate the Sharpe ratio of the window
- Return the output state to be used in the next iteration
To make sure that the calculation procedure above is correct, let's create a simple function rolling_sharpe_ratio_nb that computes the rolling Sharpe ratio using our accumulator, and compare its output to the output of another function with a totally different implementation - ReturnsAccessor.rolling_sharpe_ratio.
>>> @njit(nogil=True)
... def rolling_sharpe_ratio_nb(returns, window, minp=None, ddof=0, ann_factor=365):
... if window is None:
... window = returns.shape[0] # (1)!
... if minp is None:
... minp = window # (2)!
... out = np.empty(returns.shape, dtype=np.float_)
...
... if returns.shape[0] == 0:
... return out
...
... cumsum = 0.
... cumsum_sq = 0.
... nancnt = 0
...
... for i in range(returns.shape[0]):
... in_state = RollSharpeAIS(
... i=i,
... ret=returns[i],
... pre_window_ret=returns[i - window] if i - window >= 0 else np.nan,
... cumsum=cumsum,
... cumsum_sq=cumsum_sq,
... nancnt=nancnt,
... window=window,
... minp=minp,
... ddof=ddof,
... ann_factor=ann_factor
... )
...
... out_state = rolling_sharpe_acc_nb(in_state)
...
... cumsum = out_state.cumsum
... cumsum_sq = out_state.cumsum_sq
... nancnt = out_state.nancnt
... out[i] = out_state.value
...
... return out
>>> ann_factor = vbt.pd_acc.returns.get_ann_factor(freq='1h') # (3)!
>>> returns = close['BTCUSDT'].vbt.to_returns() # (4)!
>>> np.testing.assert_allclose(
... rolling_sharpe_ratio_nb(
... returns=returns.values,
... window=10,
... ddof=1, # (5)!
... ann_factor=ann_factor),
... returns.vbt.returns(freq='1h').rolling_sharpe_ratio(10).values
... )
- Window size of
Nonemakes the window expanding - Minimum number of observations of
Nonedefaults to the window size - Get the annualization factor using ReturnsAccessor.get_ann_factor
- Calculate the returns using GenericAccessor.to_returns
- The default
ddofis1in accessors (as it does Pandas) and0in Numba-compiled functions (as it does NumPy)
We're good - both functions return identical arrays!
Callbacks¶
In a contextualized simulation using from_order_func_nb, there is a number of callbacks we can use to define our logic in. The simulator takes a shape target_shape and iterates over columns and rows of this shape in a specific fashion. You can imagine this shape being a two-dimensional array where columns are assets (denoted as col) and rows are time steps (denoted as i). For each element of this shape, we call an order function. This is similar to how we trade in the real world: 1 trade on BTC and 0 trades on ETH yesterday, 0 trades on BTC and 0 trades on ETH today, etc.
| Date | BTCUSDT (col=0) | ETHUSDT (col=1) |
|---|---|---|
2020-01-01 (i=0) | 1 | 0 |
2020-01-02 (i=1) | 0 | 1 |
| ... | ... | ... |
today (i=n) | 1 | 1 |
Since the simulator suddenly works on multiple columns, the information we need to manage to run the streaming SuperTrend such as cumsum and cumsum_sq should be defined per column. This means we're scratching scalars in favor of one-dimensional arrays. Why arrays and not lists, dicts, or tuples? Because arrays are faster than lists and dicts, can be modified in contrast to tuples, and they are native data structures in Numba, which makes them more than suited to hold and modify data.
In traditional backtesting, we usually store our own variables such as arrays on the instance we're working on. But during simulation with vectorbt, we don't have classes and instances (well, Numba has a concept of jitted classes, but they are too heavy-weight): the only way to pass any information around is by letting a callback return them as a tuple to be consumed by other callbacks down the execution stack. As you can imagine, managing large tuples is not quite intuitive. The best way is to create a named tuple, which acts as a container (also called "memory") and is perfectly acceptable by Numba. We can then access any array conveniently by its name.
So, where do we define this memory? Whenever the simulator starts a new simulation, it first calls the pre_sim_func_nb callback, which is just a regular pre-processing function called prior to the main simulation procedure. Whatever this function returns gets passed to other callbacks. Sounds like a perfect place, right?
>>> class Memory(tp.NamedTuple): # (1)!
... nobs: tp.Array1d
... old_wt: tp.Array1d
... weighted_avg: tp.Array1d
... prev_upper: tp.Array1d
... prev_lower: tp.Array1d
... prev_dir_: tp.Array1d
... cumsum: tp.Array1d
... cumsum_sq: tp.Array1d
... nancnt: tp.Array1d
... was_entry: tp.Array1d
... was_exit: tp.Array1d
>>> @njit(nogil=True)
... def pre_sim_func_nb(c):
... memory = Memory( # (2)!
... nobs=np.full(c.target_shape[1], 0, dtype=np.int_),
... old_wt=np.full(c.target_shape[1], 1., dtype=np.float_),
... weighted_avg=np.full(c.target_shape[1], np.nan, dtype=np.float_),
... prev_upper=np.full(c.target_shape[1], np.nan, dtype=np.float_),
... prev_lower=np.full(c.target_shape[1], np.nan, dtype=np.float_),
... prev_dir_=np.full(c.target_shape[1], np.nan, dtype=np.float_),
... cumsum=np.full(c.target_shape[1], 0., dtype=np.float_),
... cumsum_sq=np.full(c.target_shape[1], 0., dtype=np.float_),
... nancnt=np.full(c.target_shape[1], 0, dtype=np.int_),
... was_entry=np.full(c.target_shape[1], False, dtype=np.bool_),
... was_exit=np.full(c.target_shape[1], False, dtype=np.bool_)
... )
... return (memory,)
- Container for our variables
- Initialize variables and put them into the container. Notice how all variables have the same length as we have the number of columns -
target_shape[1].
The memory returned by the simulation pre-processing function gets automatically prepended to the arguments of every other callback, unless some callbacks higher in the call hierarchy decide not to do so and limit exposure to the memory. Let's write the main part of our simulation - the order function, which takes the surrounding context, the memory, and the parameter values passed by the user, calculates the current SuperTrend values, and finally, uses them to decide whether to enter or exit the position. This signal gets stored in the memory and gets only executed at the next time step (this was our initial requirement):
>>> @njit(nogil=True)
... def order_func_nb(c, memory, period, multiplier):
... # (1)!
... is_entry = memory.was_entry[c.col]
... is_exit = memory.was_exit[c.col]
...
... # (2)!
... in_state = SuperTrendAIS(
... i=c.i,
... high=c.high[c.i, c.col],
... low=c.low[c.i, c.col],
... close=c.close[c.i, c.col],
... prev_close=c.close[c.i - 1, c.col] if c.i > 0 else np.nan,
... prev_upper=memory.prev_upper[c.col],
... prev_lower=memory.prev_lower[c.col],
... prev_dir_=memory.prev_dir_[c.col],
... nobs=memory.nobs[c.col],
... weighted_avg=memory.weighted_avg[c.col],
... old_wt=memory.old_wt[c.col],
... period=period,
... multiplier=multiplier
... )
...
... # (3)!
... out_state = superfast_supertrend_acc_nb(in_state)
...
... # (4)!
... memory.nobs[c.col] = out_state.nobs
... memory.weighted_avg[c.col] = out_state.weighted_avg
... memory.old_wt[c.col] = out_state.old_wt
... memory.prev_upper[c.col] = out_state.upper
... memory.prev_lower[c.col] = out_state.lower
... memory.prev_dir_[c.col] = out_state.dir_
... memory.was_entry[c.col] = not np.isnan(out_state.long)
... memory.was_exit[c.col] = not np.isnan(out_state.short)
...
... # (5)!
... in_position = c.position_now > 0
... if is_entry and not in_position:
... size = np.inf
... elif is_exit and in_position:
... size = -np.inf
... else:
... size = np.nan
... return vbt.pf_nb.order_nb(
... size=size,
... direction=vbt.pf_enums.Direction.LongOnly,
... fees=0.001
... )
- Access the signals generated at the previous time step (= shifting)
- Build the input state for
superfast_supertrend_acc_nbfrom the surrounding context and memory - Run the SuperTrend accumulator for this step
- Write the returned state back into the memory
- Decide whether to buy (
np.inf), sell (-np.inf), or do nothing (np.nan)
Hint
If the execution time has to be shifted by more than one tick, consider creating a full array for long and short values returned by superfast_supertrend_acc_nb and access any previous element in those arrays to generate a signal.
If an order decision (such as is_entry) is based on an information from an array (such as memory.was_entry), temporarily store the element in a const variable - Numba loves it.
The last callback is the segment post-processing function. A segment is simply a group of columns at a single time step, mostly for managing orders of assets that share the same capital or are connected by any other means. Since our portfolio isn't grouped, every column (BTCUSDT and ETHUSDT) has its own group, and thus each segment contains only one column. After all columns in a segment have been processed, the simulator updates the current group value and the return. The latter is used by our callback to calculate the Sharpe ratio:
>>> @njit(nogil=True)
... def post_segment_func_nb(c, memory, ann_factor):
... for col in range(c.from_col, c.to_col): # (1)!
... in_state = RollSharpeAIS(
... i=c.i,
... ret=c.last_return[col], # (2)!
... pre_window_ret=np.nan,
... cumsum=memory.cumsum[col],
... cumsum_sq=memory.cumsum_sq[col],
... nancnt=memory.nancnt[col],
... window=c.i + 1, # (3)!
... minp=0,
... ddof=1,
... ann_factor=ann_factor
... )
... out_state = rolling_sharpe_acc_nb(in_state)
... memory.cumsum[col] = out_state.cumsum
... memory.cumsum_sq[col] = out_state.cumsum_sq
... memory.nancnt[col] = out_state.nancnt
... c.in_outputs.sharpe[col] = out_state.value # (4)!
- Iterate over all columns in the current segment. In our case, each segment has only one column.
- Get the return effective at the end of the current time step
- Expanding window
- Write the Sharpe value to the in-output array defined below
Here's a short illustration of what calls what:
flowchart TD;
id1["pre_sim_func_nb"]
id1 -->|"memory"| id2;
id1 -->|"memory"| id8;
subgraph " "
id2["order_func_nb"]
id3["superfast_supertrend_acc_nb"]
id4["SuperTrend"]
id5["Signal"]
id6["Order"]
id2 -->|"calls"| id3;
id3 -->|"calculates"| id4;
id4 -->|"generates"| id5;
id5 -->|"issues"| id6;
id7["Return"]
id6 -->|"updates"| id7;
id7 -->|"consumed by"| id8;
id8["post_segment_func_nb"]
id9["rolling_sharpe_acc_nb"]
id10["Sharpe"]
id8 -->|"calls"| id9;
id9 -->|"calculates"| id10;
end(Reload the page if the diagram doesn't show up)
Info
The operation flow within the rectangle is executed at each time step.
Pipeline¶
Let's put all the parts together and define our super-flexible pipeline:
>>> class InOutputs(tp.NamedTuple): # (1)!
... sharpe: tp.Array1d
>>> @njit(nogil=True)
... def ctx_pipeline_nb(high, low, close,
... periods=np.asarray([7]),
... multipliers=np.asarray([3]),
... ann_factor=365):
...
... in_outputs = InOutputs(sharpe=np.empty(close.shape[1], dtype=np.float_))
... sharpe = np.empty(periods.size * close.shape[1], dtype=np.float_)
... group_lens = np.full(close.shape[1], 1)
... init_cash = 100.
... k = 0
...
... for i in range(periods.size):
... sim_out = vbt.pf_nb.from_order_func_nb(
... target_shape=close.shape,
... group_lens=group_lens,
... cash_sharing=False,
... init_cash=init_cash,
... pre_sim_func_nb=pre_sim_func_nb,
... order_func_nb=order_func_nb,
... order_args=(periods[i], multipliers[i]),
... post_segment_func_nb=post_segment_func_nb,
... post_segment_args=(ann_factor,),
... high=high,
... low=low,
... close=close,
... in_outputs=in_outputs,
... fill_pos_info=False, # (2)!
... max_order_records=0 # (3)!
... )
... sharpe[k:k + close.shape[1]] = in_outputs.sharpe
... k += close.shape[1]
...
... return sharpe
- A named tuple with any array that we want to write during the simulation and have access to after the simulation
- Disable filling position records to speed up the simulation
- Disable filling order records to speed up the simulation
The function has the same signature as pipeline_nb, and gladly, produces the same results!
>>> ctx_pipeline_nb(
... high.values,
... low.values,
... close.values,
... ann_factor=ann_factor
... )
array([1.521221, 2.25850084])
>>> chunked_ctx_pipeline_nb = nb_chunked(ctx_pipeline_nb)
>>> chunked_ctx_pipeline_nb(
... high.values,
... low.values,
... close.values,
... periods=period_product[:4],
... multipliers=multiplier_product[:4],
... ann_factor=ann_factor,
... _n_chunks=2,
... _merge_kwargs=dict(input_columns=close.columns)
... )
st_period st_multiplier symbol
4 2.0 BTCUSDT 0.451699
ETHUSDT 1.391032
2.1 BTCUSDT 0.495387
ETHUSDT 1.134741
2.2 BTCUSDT 0.985946
ETHUSDT 0.955616
2.3 BTCUSDT 1.193179
ETHUSDT 1.307505
dtype: float64
But in contrast to the previous pipeline, it's several times slower:
>>> %%timeit
>>> chunked_ctx_pipeline_nb(
... high.values,
... low.values,
... close.values,
... periods=period_product,
... multipliers=multiplier_product,
... ann_factor=ann_factor,
... _merge_kwargs=dict(input_columns=close.columns)
... )
6.4 s ± 45.7 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)
>>> %%timeit
>>> chunked_ctx_pipeline_nb(
... high.values,
... low.values,
... close.values,
... periods=period_product,
... multipliers=multiplier_product,
... ann_factor=ann_factor,
... _execute_kwargs=dict(engine="dask"),
... _merge_kwargs=dict(input_columns=close.columns)
... )
1.38 s ± 26.1 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)
We traded in a bit of performance for full flexibility. But even in this constellation, event-driven backtesting of a full grid of parameter combinations with vectorbt is on par with a single SuperTrend calculation with Pandas
Bonus: Own simulator¶
If all you care is the best possible performance, you have a perfect streaming algorithm, and you know exactly how to calculate the metrics of interest on the fly, you probably can drop the simulation with the Portfolio class entirely and define the entire logic in a collection of primitive but purified and hyperfast Numba-compiled for-loops. In this case, you can directly use the vectorbt's core functionality for order execution:
>>> @njit(nogil=True)
... def raw_pipeline_nb(high, low, close,
... periods=np.array([7]),
... multipliers=np.array([3]),
... ann_factor=365):
... out = np.empty(periods.size * close.shape[1], dtype=np.float_) # (1)!
...
... if close.shape[0] == 0:
... return out
...
... for k in range(len(periods)): # (2)!
...
... for col in range(close.shape[1]): # (3)!
... # (4)!
... nobs = 0
... old_wt = 1.
... weighted_avg = np.nan
... prev_close_ = np.nan
... prev_upper = np.nan
... prev_lower = np.nan
... prev_dir_ = 1
... cumsum = 0.
... cumsum_sq = 0.
... nancnt = 0
... was_entry = False
... was_exit = False
...
... # (5)!
... init_cash = 100.
... cash = init_cash
... position = 0.
... debt = 0.
... locked_cash = 0.
... free_cash = init_cash
... val_price = np.nan
... value = init_cash
... prev_value = init_cash
... return_ = 0.
...
... for i in range(close.shape[0]): # (6)!
... # (7)!
... is_entry = was_entry
... is_exit = was_exit
...
... st_in_state = SuperTrendAIS(
... i=i,
... high=high[i, col],
... low=low[i, col],
... close=close[i, col],
... prev_close=prev_close_,
... prev_upper=prev_upper,
... prev_lower=prev_lower,
... prev_dir_=prev_dir_,
... nobs=nobs,
... weighted_avg=weighted_avg,
... old_wt=old_wt,
... period=periods[k],
... multiplier=multipliers[k]
... )
...
... st_out_state = superfast_supertrend_acc_nb(st_in_state)
...
... nobs = st_out_state.nobs
... weighted_avg = st_out_state.weighted_avg
... old_wt = st_out_state.old_wt
... prev_close_ = close[i, col]
... prev_upper = st_out_state.upper
... prev_lower = st_out_state.lower
... prev_dir_ = st_out_state.dir_
... was_entry = not np.isnan(st_out_state.long)
... was_exit = not np.isnan(st_out_state.short)
...
... if is_entry and position == 0:
... size = np.inf
... elif is_exit and position > 0:
... size = -np.inf
... else:
... size = np.nan
...
... # (8)!
... val_price = close[i, col]
... value = cash + position * val_price
... if not np.isnan(size):
... exec_state = vbt.pf_enums.ExecState( # (9)!
... cash=cash,
... position=position,
... debt=debt,
... locked_cash=locked_cash,
... free_cash=free_cash,
... val_price=val_price,
... value=value
... )
... price_area = vbt.pf_enums.PriceArea( # (10)!
... open=np.nan,
... high=high[i, col],
... low=low[i, col],
... close=close[i, col]
... )
... order = vbt.pf_nb.order_nb( # (11)!
... size=size,
... direction=vbt.pf_enums.Direction.LongOnly,
... fees=0.001
... )
... _, new_exec_state = vbt.pf_nb.execute_order_nb( # (12)!
... exec_state, order, price_area)
... cash, position, debt, locked_cash, free_cash, val_price, value = new_exec_state
...
... value = cash + position * val_price
... return_ = vbt.ret_nb.get_return_nb(prev_value, value) # (13)!
... prev_value = value
...
... # (14)!
... sharpe_in_state = RollSharpeAIS(
... i=i,
... ret=return_,
... pre_window_ret=np.nan,
... cumsum=cumsum,
... cumsum_sq=cumsum_sq,
... nancnt=nancnt,
... window=i + 1,
... minp=0,
... ddof=1,
... ann_factor=ann_factor
... )
... sharpe_out_state = rolling_sharpe_acc_nb(sharpe_in_state)
... cumsum = sharpe_out_state.cumsum
... cumsum_sq = sharpe_out_state.cumsum_sq
... nancnt = sharpe_out_state.nancnt
... sharpe = sharpe_out_state.value
...
... out[k * close.shape[1] + col] = sharpe # (15)!
...
... return out
- The number of Sharpe ratios = the number of parameter combinations x the number of columns
- For each parameter combination (product and multiplier)
- For each column (asset)
- Define the initial values for the SuperTrend and Sharpe accumulators
- Define the initial state of the backtesting environment, such as the initial cash balance
- For each row (time step)
- Calculate the SuperTrend values for this time step, generate a signal based on them, and transform the signal into an order size
- Build and execute an order, and update the return at the end of this time step
- Pack the current state of the environment into an instance of ExecState
- Pack the current price bounds into an instance of PriceArea
- Get an instance of type Order using order_nb
- Execute the order using execute_order_nb, which returns the order result of type OrderResult and the updated state of the backtesting environment of type AccountState
- Return is the percentage change between the previous value and the current value
- Calculate the Sharpe ratio based on the updated return
- Write the Sharpe ratio of the latest time step into the output array
We just created our own simulator optimized for one particular task, and as you might have guessed, its speed is something unreal!
>>> chunked_raw_pipeline_nb = nb_chunked(raw_pipeline_nb)
>>> %%timeit
>>> chunked_raw_pipeline_nb(
... high.values,
... low.values,
... close.values,
... periods=period_product,
... multipliers=multiplier_product,
... ann_factor=ann_factor,
... _merge_kwargs=dict(input_columns=close.columns)
... )
225 ms ± 464 µs per loop (mean ± std. dev. of 7 runs, 1 loop each)
>>> %%timeit
>>> chunked_raw_pipeline_nb(
... high.values,
... low.values,
... close.values,
... periods=period_product,
... multipliers=multiplier_product,
... ann_factor=ann_factor,
... _execute_kwargs=dict(engine="dask"),
... _merge_kwargs=dict(input_columns=close.columns)
... )
54 ms ± 1.13 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)
The reason why we see a 20x jump in performance compared to the latest pipeline even though it also processed the data in a streaming fashion, is because vectorbt has to prepare the contexts for all callbacks (even those that do nothing by default) and calculate all possible metrics that the user may need. Additionally, Numba hates complex relationships between objects that are shared or passed back and forth between multiple functions, so designing an efficient order function may not be the easiest challenge.
The best in the pipeline above is that it's very memory efficient. Let's roll 100 one-year periods over the entire period (1,752,000 input data points in total), backtest the full parameter grid on each one, and animate the whole thing as a GIF - in 15 seconds!
First, we need to split the entire period into sub-periods:
>>> range_len = int(vbt.timedelta('365d') / vbt.timedelta('1h')) # (1)!
>>> splitter = vbt.Splitter.from_n_rolling( # (2)!
... high.index,
... n=100,
... length=range_len
... )
>>> roll_high = splitter.take(high, into="reset_stacked") # (3)!
>>> roll_low = splitter.take(low, into="reset_stacked")
>>> roll_close = splitter.take(close, into="reset_stacked")
>>> roll_close.columns
MultiIndex([( 0, 'BTCUSDT'),
( 0, 'ETHUSDT'),
( 1, 'BTCUSDT'),
( 1, 'ETHUSDT'),
( 2, 'BTCUSDT'),
...
(97, 'ETHUSDT'),
(98, 'BTCUSDT'),
(98, 'ETHUSDT'),
(99, 'BTCUSDT'),
(99, 'ETHUSDT')],
names=['split', 'symbol'], length=200)
>>> range_indexes = splitter.take(high.index) # (4)!
>>> range_indexes[0]
DatetimeIndex(['2020-01-01 00:00:00+00:00', '2020-01-01 01:00:00+00:00',
'2020-01-01 02:00:00+00:00', '2020-01-01 03:00:00+00:00',
'2020-01-01 04:00:00+00:00', '2020-01-01 05:00:00+00:00',
...
'2020-12-31 12:00:00+00:00', '2020-12-31 13:00:00+00:00',
'2020-12-31 14:00:00+00:00', '2020-12-31 15:00:00+00:00',
'2020-12-31 16:00:00+00:00', '2020-12-31 17:00:00+00:00'],
dtype='datetime64[ns, UTC]', name='split_0', length=8760, freq=None)
- Get the number of hours in a year
- Create an instance of Splitter
- Split the DataFrame into chunks and stack those chunks into one DataFrame by resetting its index. We reset the index because otherwise the operation would produce many NaNs.
- We also want to know the index of each split. Thus, split it in the same way as we did above, but instead of stacking, store it in a Series indexed by split label.
Next, generate the Sharpe values:
>>> sharpe_ratios = chunked_raw_pipeline_nb(
... roll_high.values,
... roll_low.values,
... roll_close.values,
... periods=period_product,
... multipliers=multiplier_product,
... ann_factor=ann_factor,
... _execute_kwargs=dict(engine="dask"),
... _merge_kwargs=dict(input_columns=roll_close.columns) # (1)!
... )
>>> sharpe_ratios
st_period st_multiplier split symbol
4 2.0 0 BTCUSDT 1.751331
ETHUSDT 2.479750
1 BTCUSDT 1.847095
ETHUSDT 2.736193
2 BTCUSDT 1.739149
...
19 4.0 97 ETHUSDT 1.503001
98 BTCUSDT 0.954932
ETHUSDT 1.204134
99 BTCUSDT 0.818209
ETHUSDT 1.191223
Length: 67200, dtype: float64
- Don't forget to pass the correct columns
67,200 backtests in one second
When plotting a heatmap for each sub-period, we will use the Sharpe ratio of holding during that period as a mid-point of the colorscale, such that any blue-tinted point indicates that the parameter combination performed better than the market, and any red-tinted point indicates that the combination performed less well. For this, we need the Sharpe of holding:
>>> pf_hold = vbt.Portfolio.from_holding(roll_close, freq='1h')
>>> sharpe_ratios_hold = pf_hold.sharpe_ratio
>>> sharpe_ratios_hold
split symbol
0 BTCUSDT 2.229122
ETHUSDT 2.370132
1 BTCUSDT 2.298050
ETHUSDT 2.611722
2 BTCUSDT 2.351417
...
97 ETHUSDT 2.315863
98 BTCUSDT 1.124489
ETHUSDT 2.114297
99 BTCUSDT 0.975638
ETHUSDT 2.008839
Name: sharpe_ratio, Length: 200, dtype: float64
Info
Notice how this multi-index lists no parameter combinations: the performance of holding isn't dependent on our indicator in any way.
Next, let's create a function that plots a sub-period:
>>> def plot_subperiod_sharpe(index,
... sharpe_ratios,
... sharpe_ratios_hold,
... range_indexes,
... symbol):
... split = index[0]
... sharpe_ratios = sharpe_ratios.xs( # (1)!
... symbol,
... level='symbol',
... drop_level=True)
... sharpe_ratios = sharpe_ratios.xs( # (2)!
... split,
... level='split',
... drop_level=True)
... start_date = range_indexes[split][0]
... end_date = range_indexes[split][-1]
... return sharpe_ratios.vbt.heatmap(
... x_level='st_period',
... y_level='st_multiplier',
... title="{} - {}".format( # (3)!
... start_date.strftime("%d %b, %Y %H:%M:%S"),
... end_date.strftime("%d %b, %Y %H:%M:%S")
... ),
... trace_kwargs=dict( # (4)!
... zmin=sharpe_ratios.min(),
... zmid=sharpe_ratios_hold[(split, symbol)],
... zmax=sharpe_ratios.max(),
... colorscale='Spectral'
... )
... )
- Select the symbol (we can only plot one at a time)
- Select the sub-period by its split index
- Title with the start and end date of the sub-period
- Set up the colorscale of the heatmap here
Finally, use save_animation to iterate over each split index, plot the heatmap of the sub-period, and append it as a PNG image to the GIF file:
>>> fname = 'raw_pipeline.gif'
>>> level_idx = sharpe_ratios.index.names.index('split')
>>> split_indices = sharpe_ratios.index.levels[level_idx]
>>> vbt.save_animation(
... fname,
... split_indices,
... plot_subperiod_sharpe, # (1)!
... sharpe_ratios, # (2)!
... sharpe_ratios_hold,
... range_indexes,
... 'BTCUSDT',
... delta=1, # (3)!
... fps=7,
... writer_kwargs=dict(loop=0) # (4)!
... )
- Plotting function
- Variable arguments passed to the plotting function
- Keyword arguments for setting up the GIF
- Loop indefinitely
>>> from IPython.display import Image, display
>>> with open(fname,'rb') as f:
... display(Image(data=f.read(), format='png'))

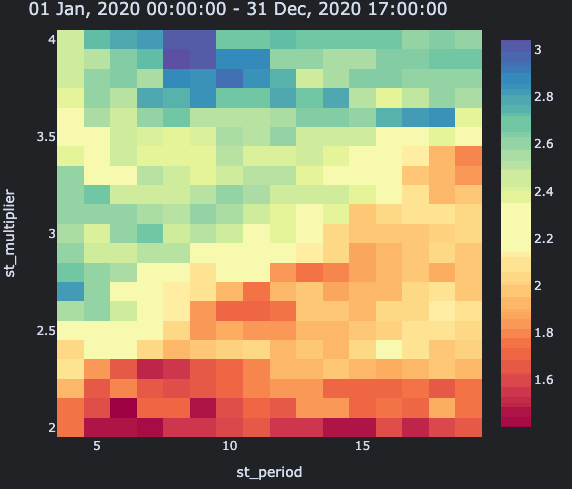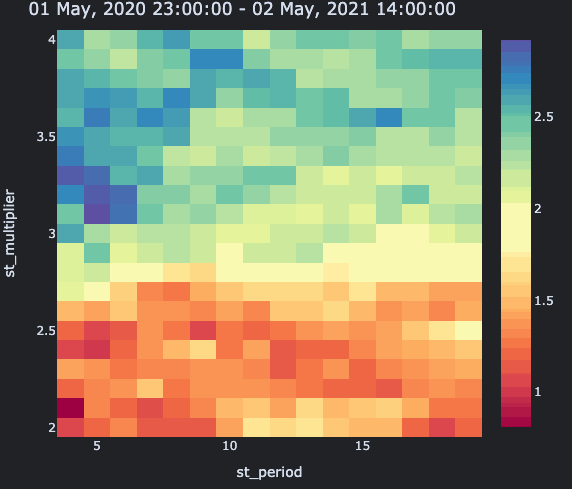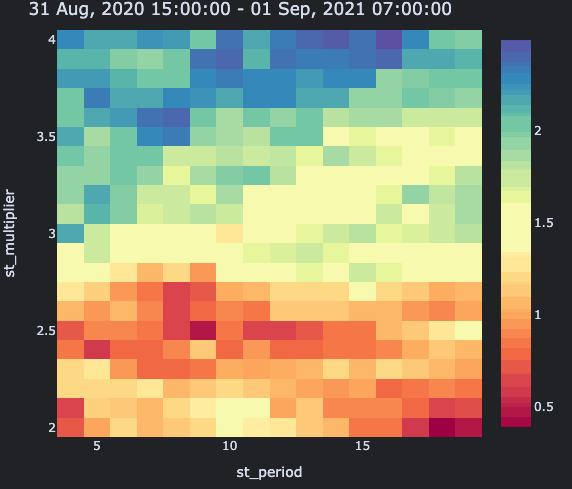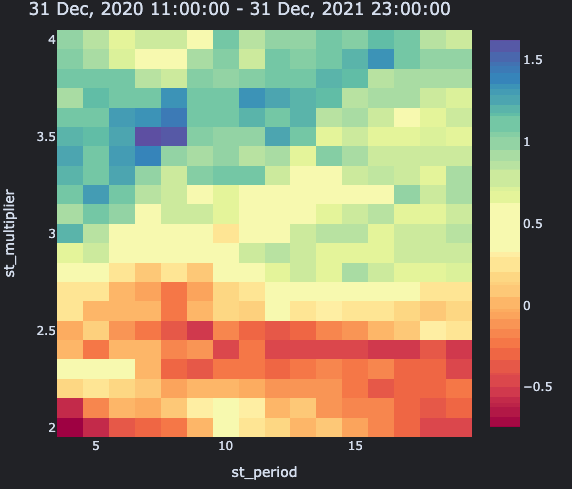
Everything bluer than yellow beats the market. Just don't pick any value at the bottom
Summary¶
We covered a lot of territories, let's digest what we have learned so far.
A pipeline is a process that takes data and transforms it into insights. Such a process can be realized through a set of totally different pipeline designs, and you can always count on vectorbt during the development of each one.
The easiest-to-use class of pipelines in vectorbt deploys two main components: indicator (such as SuperTrend) and simulator (such as Portfolio.from_signals); both can be developed, tweaked, and run independently of each other. This modular design yields the highest flexibility when signals and order execution aren't path-dependent. The only drawback is a high memory consumption, which can only be mitigated by chunking - splitting data and/or parameters into bunches that are processed sequentially (loop) or in parallel. Chunking also enables other two perks to utilize all cores: multiprocessing and multithreading. But the latter can only work when the entire pipeline is Numba-compiled and can release the GIL. Luckily for us, vectorbt offers a lot of utilities that can be used from within Numba, thus don't be afraid of writing the entire pipeline with Numba - it's easier than it seems!
But once signals become dependent upon trades made previously, both components must be merged into a monolithic workflow. Such workflows are possible using contextualized simulation, such as with Portfolio.from_order_func, which lets us inject our custom trading logic into the simulator itself using callbacks and contexts. This approach is very similar to the event-driven backtesting approach used by many backtesting frameworks, such as backtrader. The only difference lies in storing and managing information, which is done using named tuples and arrays, as opposed to classes and variables. Such pipelines offer the greatest flexibility but are considerably slower than the modular ones (although they would still leave most other backtesting software in the dust). To dramatically increase performance, you can switch to a lower-level API and implement the simulator by yourself. Sounds scary? It shouldn't because every simulator is just a bunch of regular for-loops and order management commands.
At the end of the day, you should pick the design that best suits your needs. There is no reason to spend days designing a perfect pipeline if all it does is save you 5 minutes, right? But at least you will learn how to design efficient algorithms in Python that can compete with top-notch algo-trading systems written in Java.
As always, happy coding